The €uro has been lately under some depreciation pressures as the Euro Area economy struggles to accelerate its economic output and wider political instability in France has been slowing down the economic growth agenda, while also the German economy has been stagnating with severe repercussions across the automaker industry, the top industrial sector of the German economy. It’d fair to argue that not everything has been rosier in Europe, considering that 2024 has also been the year with the highest number of political elections all around the world, this should provide a little comfort in hoping that going forward political instability will subside and the economy can liberate itself for business. With all this uncertainty the €uro has come under some pressure also considering money market interest rate differentials between the $dollar and the €uro, with the ECB going forward with Euribor cuts, so to stimulate the economy and relieve pressures on businesses and consumers.
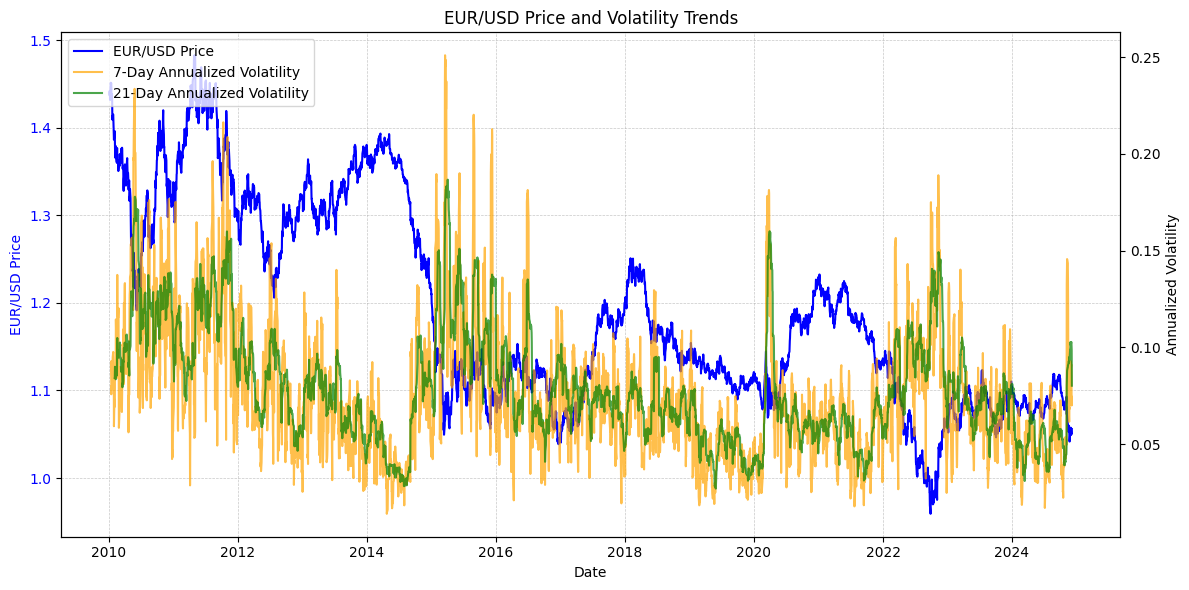
In this article, the EUR/USD time-series conditional volatility and January’25 option chain Greeks have been analysed and inference of their econometric volatility models have been compared in order to gather what option markets implied volatility has been actually pricing what could be the EUR/USD exchange rate in one month time. For starters in the graph, the EUR/USD time series has been elaborated on 7-day and 21-day Annualised volatility trends overlayed with the EUR/USD trendline and it’s possible to see how in the second half of 2024 EUR/USD the annualised volatility lines have been rising upward toward 10% and 15% while EUR/USD trendline has been drifting lower, with the €uro depreciating.
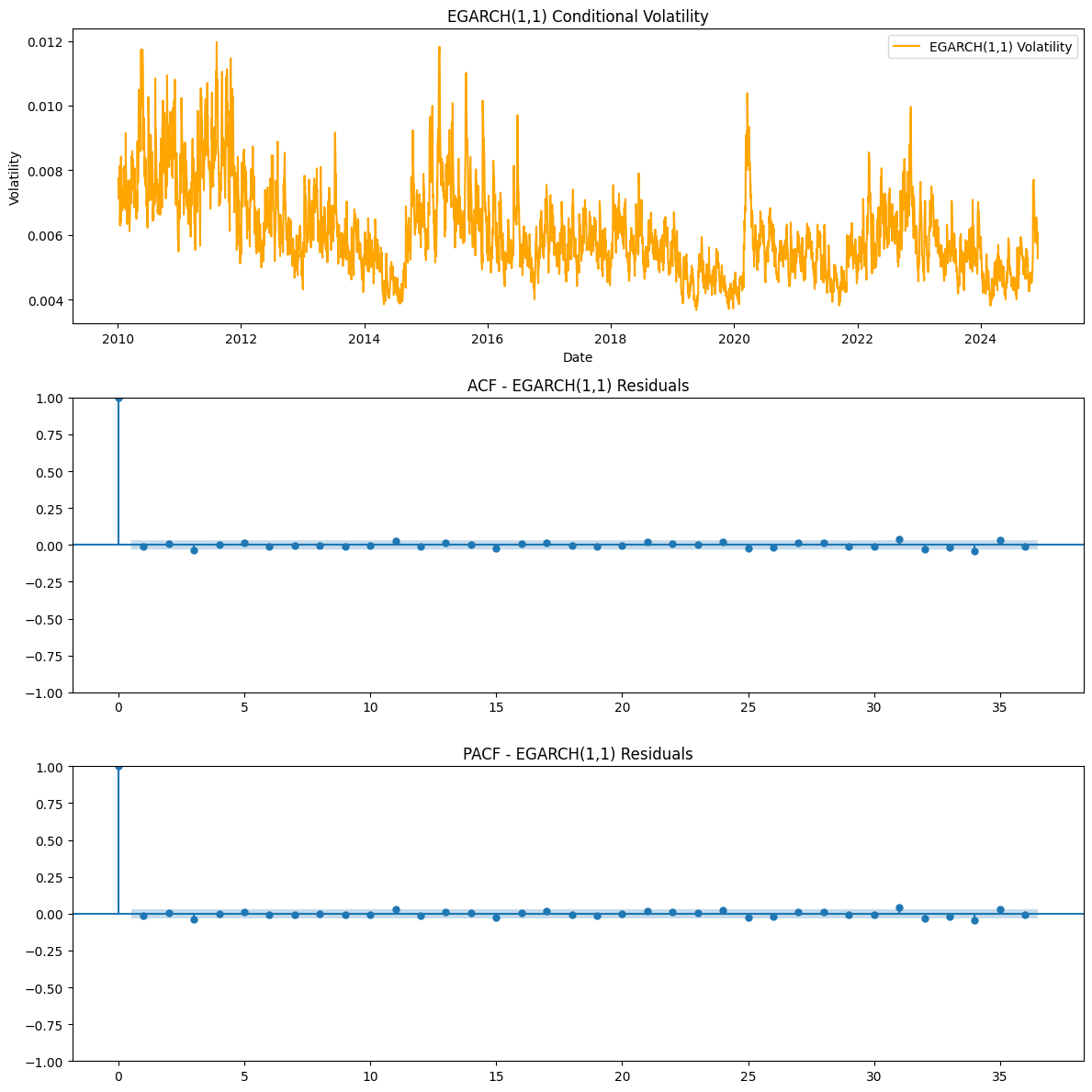
To evaluate with more accuracy the EUR/USD time series conditional volatility similar econometrics models have been implemented: GARCH(1,1) and EGARCH(1,1). The EGARCH has displayed a very good fit as an econometric model for understanding EUR/USD volatility patterns, data of EGARCH display time-series ACF and PACF residuals are stationary, and the Log-likelihood value confirms a very good fit, while the Alpha 0.2285 parameter explains consistent past shock and new information inference of volatility patterns, while the Beta 0.9109 gives a consistent data of how volatility can be persistent across time, feeding through the data and repeating its patterns.
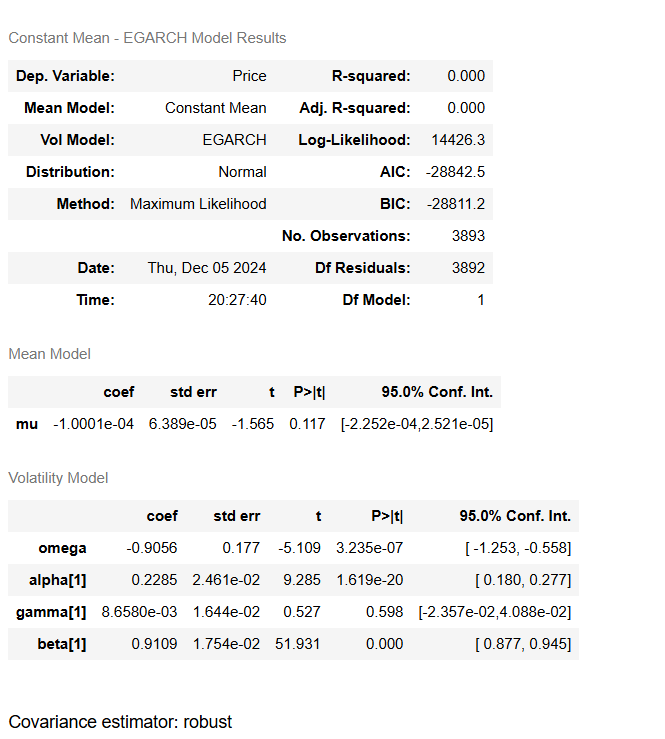
For the GARCH(1,1), the estimated constant mean mu (μ): -0.0074112 of the series. The p-value (0.376) indicates that it is not statistically significant, meaning the mean is not significantly different from zero. omega (ω): 0.001407 is the constant term in the variance equation. It determines the baseline level of volatility. It is statistically significant (p-value = 0.039), indicating its contribution to the model. Alpha[1] (α1): 0.0324 The coefficient for the lagged squared residual captures the impact of past shocks on current volatility. It is highly statistically significant (p-value = 0.002), showing past shocks affect current volatility. Beta[1] (β1): 0.9639 The coefficient for the lagged conditional variance captures the persistence of volatility over time. It is also highly statistically significant (p-value < 0.0001). The high value (~0.964) indicates a strong persistence of volatility. The persistence of volatility can be measured as α1+β1=0.0324+0.9639=0.9963, This value is very close to 1, indicating that volatility is highly persistent, implies that volatility in EUR/USD exchange rates remains elevated for long periods after a shock, consistent with common characteristics of financial time series.
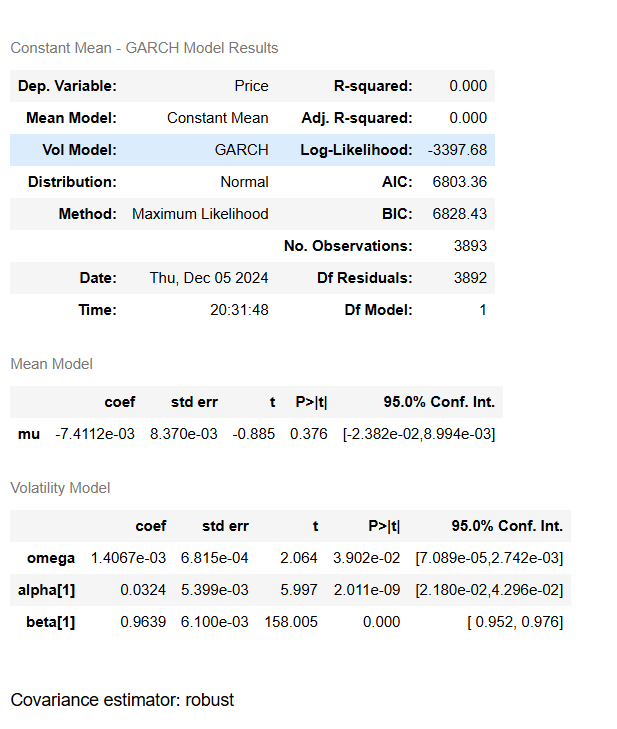
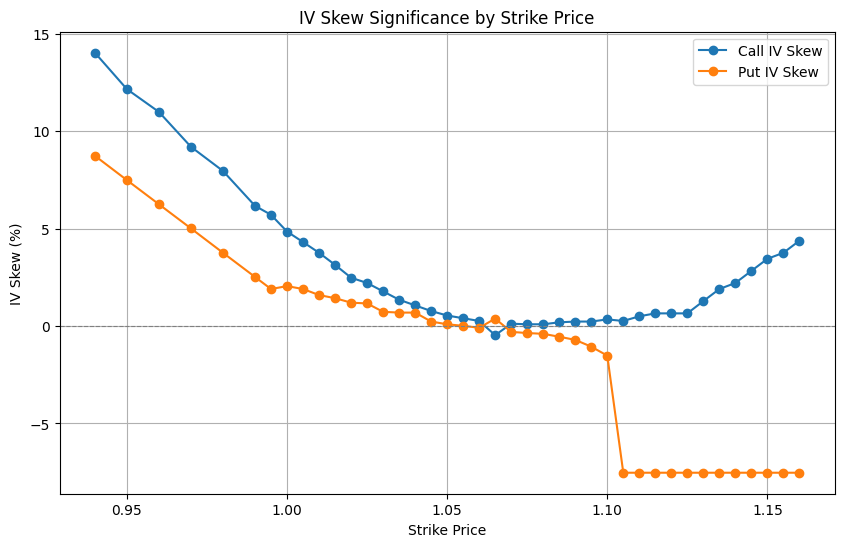
IV Skew: The first graph illustrates the implied volatility (IV) skew across strike prices for call and put options. At lower strike prices, call options exhibit higher IV, reflecting demand for out-of-the-money (OTM) calls as a hedge against upward moves in EUR/USD. Conversely, put options have lower IV at those strikes. Around at-the-money (ATM) levels (strike ~1.10), the IV converges before put IV drops sharply beyond this threshold, highlighting a relative preference for protective puts in OTM regions.
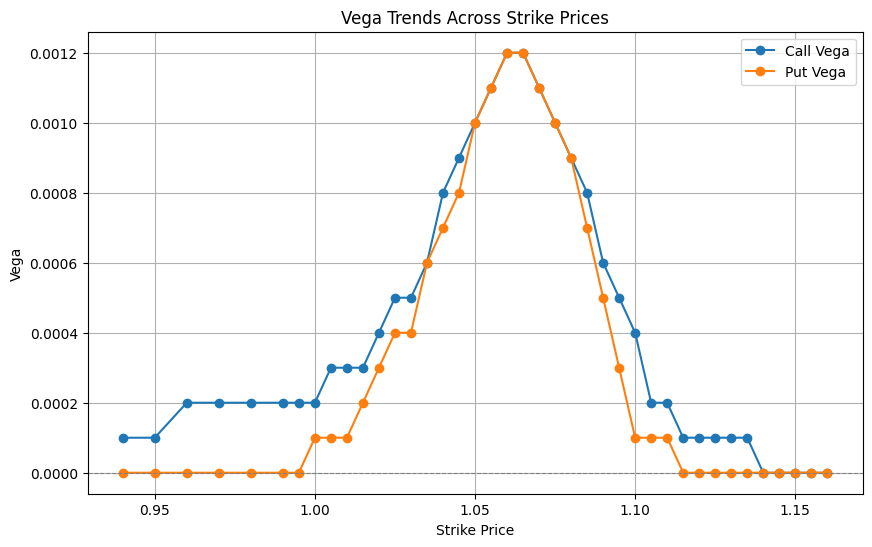
Vega: The Vega graph shows a peak for both calls and puts near ATM strike prices (~1.10). This is typical as Vega is highest when options are ATM, reflecting their sensitivity to changes in volatility. Calls and puts exhibit symmetrical behaviour, with Vega diminishing for deeply in-the-money (ITM) and OTM options. This suggests a balanced volatility sensitivity across the board.
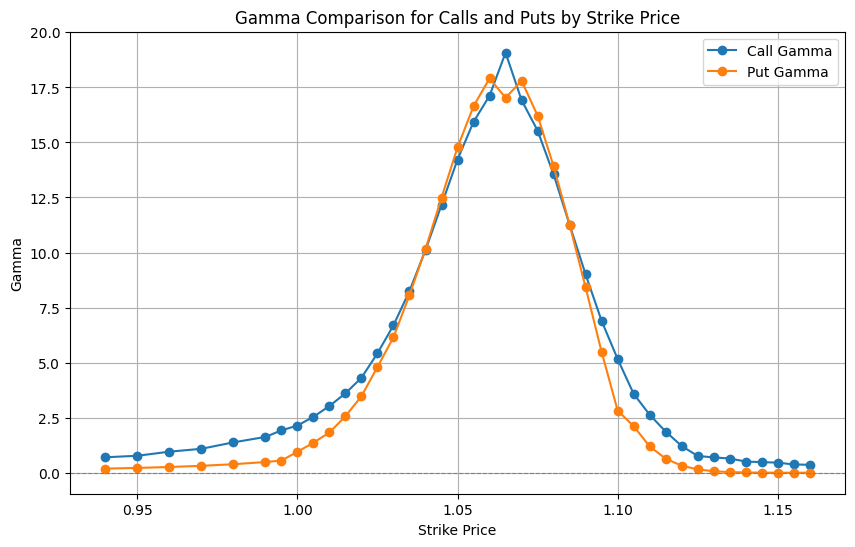
Gamma: The Gamma plot peaks sharply near the ATM strike (~1.10) for both call and put options, emphasizing heightened sensitivity to changes in the underlying price for options close to ATM. Gamma values taper off symmetrically as options move ITM or OTM, consistent with typical option behaviour. This highlights that small price changes in EUR/USD around 1.10 will significantly affect Delta.
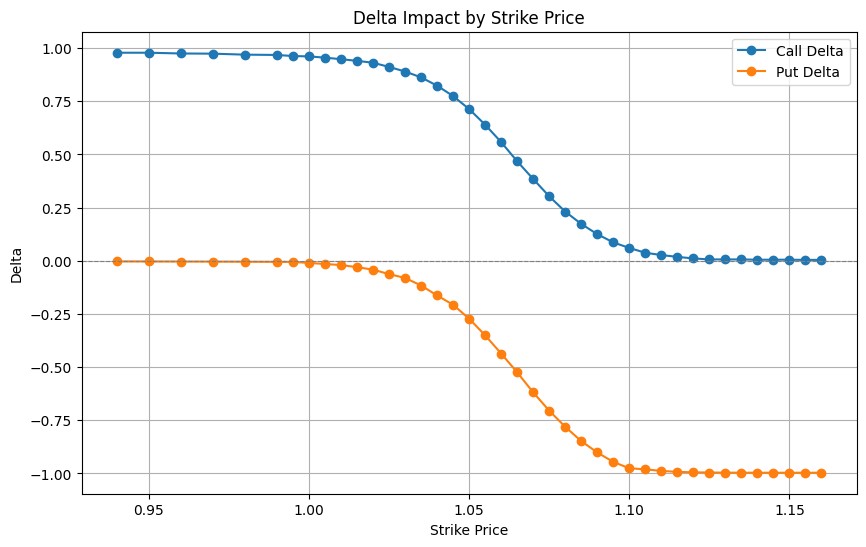
Delta: The Delta graph follows an S-curve for calls and an inverse S-curve for puts. At low strike prices, call Delta is close to 1 (deep ITM), while put Delta approaches -1 (deep ITM for puts). Around the ATM strike (~1.10), Delta transitions rapidly from 0 to 1 for calls and 0 to -1 for puts, reflecting the transition of moneyness.
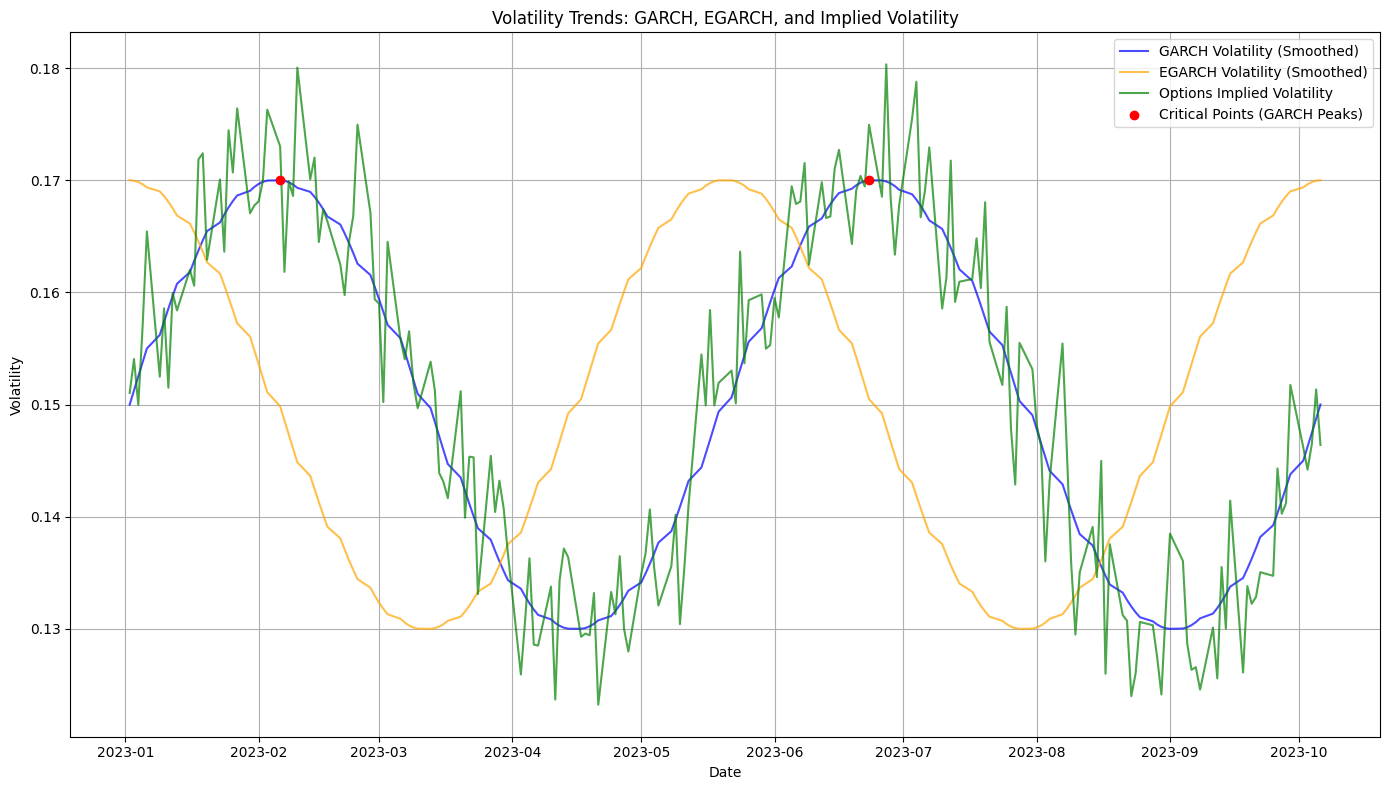
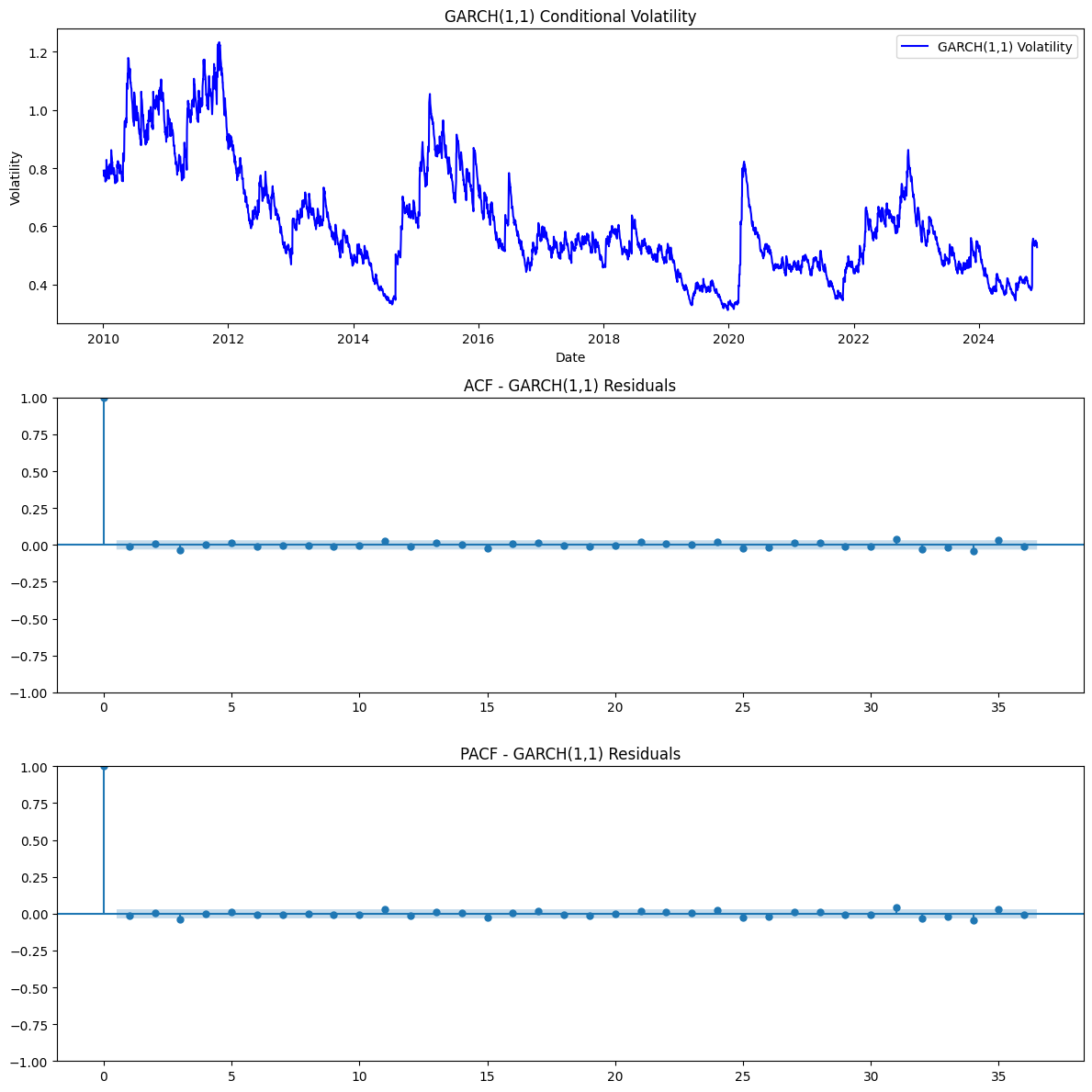
GARCH Volatility (Blue Line): This shows volatility trends modelled using a GARCH approach. It provides a smoothed representation of historical volatility and is generally consistent with market patterns. EGARCH Volatility (Orange Line): EGARCH allows for asymmetric impacts of positive and negative shocks. The orange line shows a different smoothing pattern compared to GARCH, with some periods of divergence, especially during volatility spikes. Implied Volatility (Green Line): The IV represents market expectations of future volatility. It is more volatile and reacts quickly to changes in market conditions (e.g., geopolitical events or economic data releases). Critical Points (Red Dots): The red dots mark peaks in GARCH volatility, corresponding to periods of heightened market turbulence. These points align, to some extent, with IV spikes, confirming that GARCH can capture broader trends.
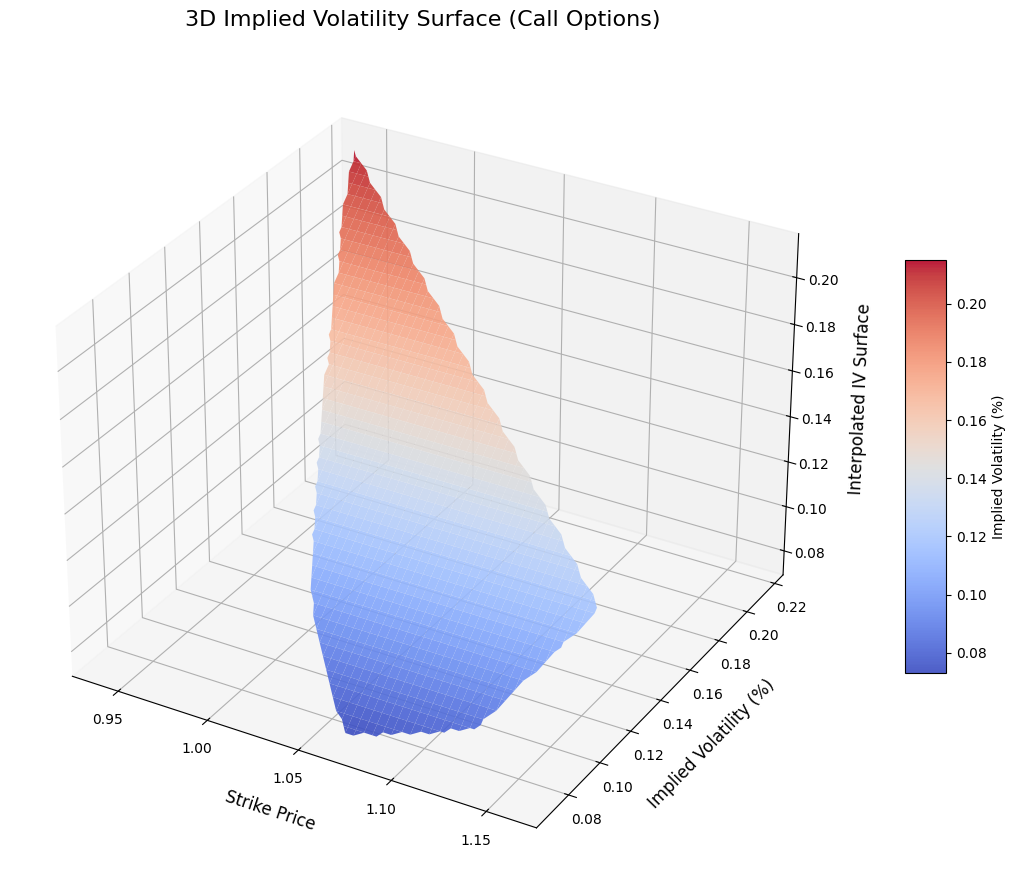
The IV surface confirms the interplay between implied volatility and the Greeks. Peaks and steep gradients around ATM strikes align with higher Delta sensitivity, Gamma peaks, and Vega relevance. The IV skew at OTM and ITM strikes suggests hedging and speculative behaviour unique to the EUR/USD options market. This analysis highlights how IV surfaces complement Greek analyses, offering insights into market expectations and risk dynamics.
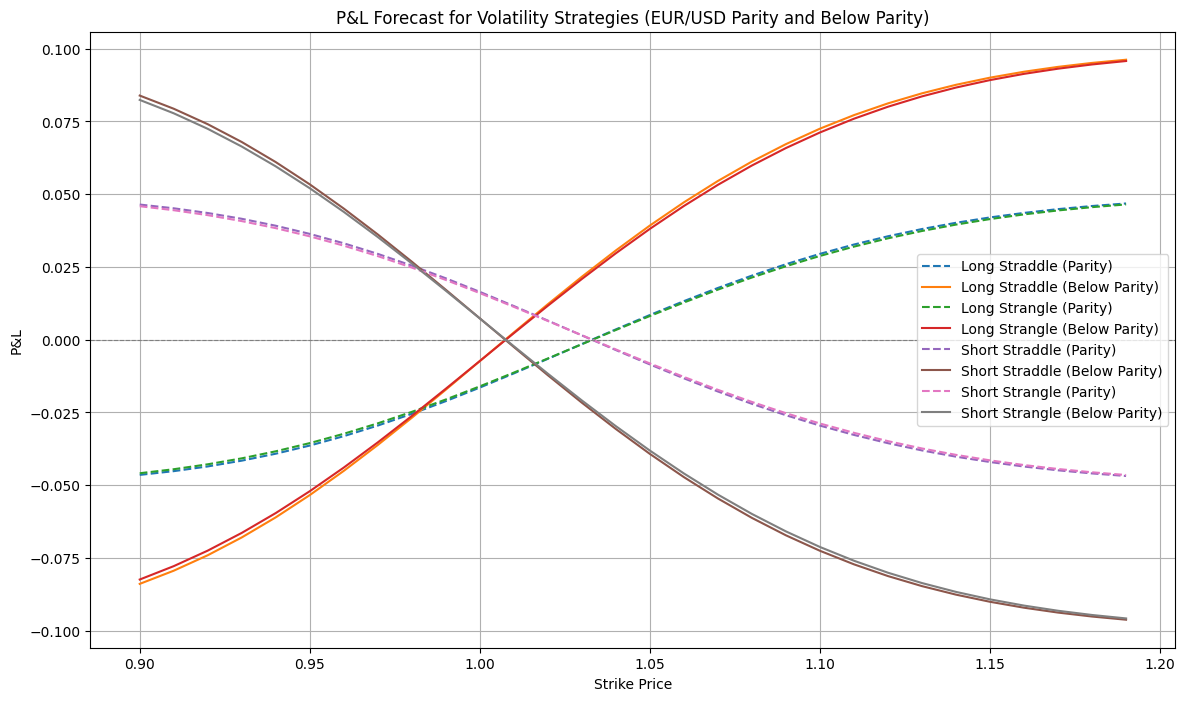
This graph illustrates the simulated P&L outcomes for various options strategies on EUR/USD at parity (1.00) and below parity. The long straddle and long strangle strategies profit from high volatility, with potential gains increasing significantly as the EUR/USD deviates from the strike price in either direction. In contrast, the short straddle and short strangle strategies benefit from low volatility and stable prices near the strike but suffer large losses if the exchange rate moves significantly. Strategies at parity (1.00) show balanced risk/reward symmetry around this critical level, while those below parity demonstrate a bias toward anticipating further depreciation of the EUR. This analysis highlights how volatility and directional expectations impact these strategies’ profitability.
READ MORE:

